為了加強學術交流與合作研究, 了解偏微分方程的最新研究成果和發展動态,由吉林大學王春朋教授提議,伟德线上平台和東北大學數學系聯合組織,将于2022年1月5日舉辦”2022年非線性偏微分方程”線上學術會議。本次會議邀請偏微分方程領域的優秀學者, 圍繞非線性偏微分方程前沿進展展開交流和讨論, 為青年教師和研究生提供學習和交流的平台。
會議組織者:
王春朋(主席) (吉林大學), 劉長春(吉林大學)
郭斌(吉林大學), 趙曉朋(東北大學), 段甯(東北大學)
線上騰訊會議:
會議ID: 921-809-822
會議鍊接: https://meeting.tencent.com/dm/MkjneVedoAKU
校内聯系人:郭斌 bguo@jlu.edu.cn
日程表:

報告題目與摘要:
Degenerate Elliptic Equations and Subsonic-sonic Flows in General Nozzles
王春朋(吉林大學)
This talk concerns subsonic-sonic potential flows in two dimensional nozzles, which are governed by nonlinear degenerate elliptic equations. For finitely long symmetric nozzles, it is shown that there exists a unique Lipschitz continuous subsonic-sonic flow, and the location of sonic points is classified completely.
報告人:王春朋, 伟德线上平台教授、國家傑出青年基金獲得者、全國優秀百篇博士學位論文獲得者、國務院特殊津貼專家,從事退化抛物方程和橢圓-雙曲混合型偏微分方程方面的研究。近年來主要圍繞光滑跨音速流理論研究拟線性混合型偏微分方程的适定性,在ARMA、Adv. Math., CPDE, JDE, SIAM J. Math. Anal., SIAM J. Control Optim. 等著名期刊上發表了系列重要論文。
On the Cahn-Hilliard equation with dynamic boundary condition and singular potential
吳昊(複旦大學)
We report some recent progresses on the Cahn-Hilliard equation with dynamic boundary conditions, which accounts for nontrivial short-range interactions of the binary mixture near the boundary. When the potentials take the form of physically relevant singular type, we show the well-posedness and long-time behavior of the initial boundary value problem.
報告人:吳昊, 複旦大學數學科學學院教授,博士生導師,教育部青年長江學者,上海市青年拔尖人才,主要從事偏微分方程理論方面的研究。吳教授曾主持國家自然科學基金項目,上海市自然科學基金項目等多項,榮獲第二屆中國工業與應用數學會優秀青年學者獎等,在ARMA,MMMAS,Ann. Inst. H. Poincare Anal. Non Lineaire,SIAM J. Math. Anal., Calc. Var. PDE,European J. Appl. Math., JDE等雜志發表了系列重要論文。
Global well-posedness to the 2D Cauchy problem of nonhomogeneous heat conducting Navier-Stokes and magnetohydrodynamic equations with vacuum at infinity
鐘新(西南大學)
In this talk, we investigate the 2D Cauchy problem of nonhomogeneous heat conducting magnetohydrodynamic equations in the whole plane. For the initial density allowing vacuum at infinity, we derive the global existence and uniqueness of strong solutions provided that the initial density and the initial magnetic decay not too slowly at infinity. In particular, the initial data can be arbitrarily large. The method is based on delicate spatial weighted estimates and the structural characteristic of the system under consideration. As a byproduct, we get the global existence of strong solutions to the 2D Cauchy problem for nonhomogeneous heat conducting Navier-Stokes equations with vacuum at infinity.
報告人:鐘新,西南大學數學與統計學院教授,重慶英才青年拔尖人才,重慶市巴渝學者青年學者。主要研究興趣為流體方程組解的整體适定性和奇點的形成,部分研究成果發表在 J. Math. Pures Appl.、Indiana Univ. Math. J.、Calc. Var. Partial Differential Equations、J. Math. Fluid Mech.、Nonlinearity、J. Differential Equations 等數學期刊上。主持完成或在研國家自然科學基金、中國博士後科學基金、重慶市自然科學基金等國家級和省部級科研項目8項。
Global well-posedness and decay estimates for three-dimensional compressible Navier-Stokes-Allen-Cahn system
趙曉朋(東北大學)
We study the small data global well-posedness and time-decay rates of solutions to the Cauchy problem for 3D compressible Navier-Stokes-Allen-Cahn equations via a refined pure energy method. In particular, the optimal decay rates of the higher order spatial derivatives of the solution are obtained, the
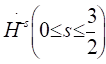
negative Sobolev norms is shown to be preserved along time evolution and enhance the decay rates.
報告人: 趙曉朋, 東北大學數學系副教授, 碩士生導師, 沈陽市拔尖人才, 主要從事非線性發展方程理論方面的研究, 部分研究成果發表在J. Nonlinear Sci.、Proc. Roy. Soc. Edinburgh Sect. A、J. Hyperbolic Diff. Equ.、Topol. Method. Nonlinear Sci.、Adv. Differential Equations等數學期刊上。 主持完成國家自然科學基金、江蘇省自然科學基金和中國博士後基金等國家級和省部級科研項目。